A compiler optimization has two basic parts. First, it needs to recognize an optimizable situation in the IR (intermediate representation), such as adjacent increments of the same variable. For the optimization to be maximally effective, the situation recognizer should cast as wide a net as possible. For example, we might broaden the applicability of an increment-coalescer by noticing that it can also operate on increments in the same basic block that are separated by non-dependent instructions, and that it can also operate on decrements. The second part of an optimization is knowing what code to replace the optimizable code with, once it has been found. In the running example, “i++; i++” becomes “i += 2”. Although some optimizations are much more sophisticated than this one, the basic idea applies everywhere. Optimizing compilers achieve good results via sequential application of a large number of optimization passes, each improving the code in some minor fashion.

Let’s look at a more interesting example. Consider this C function:

int cannot_overflow (int a)
{
  if (a==INT_MAX) return 0;
  return a+1;
}

Now build it with Clang’s undefined behavior sanitizer:

clang -S -emit-llvm -O2 cannot_overflow.c -fsanitize=undefined

Here’s the output (at the IR level) that we want to see:

In other words, the code that we want to see implements the function but has no extra UBSan logic — overflow checking is not required because the function obviously cannot execute an undefined overflow regardless of the value of the argument. (Actually, due to elimination of the branch, the LLVM code can execute an undefined overflow. This is OK since an undefined overflow in LLVM only affects the result of the operation, in contrast with the unbounded consequences of UB at the C level.)

The code above is what we want. What we actually get — using Clang/LLVM as of today, and also Clang/LLVM 3.4 — is this:

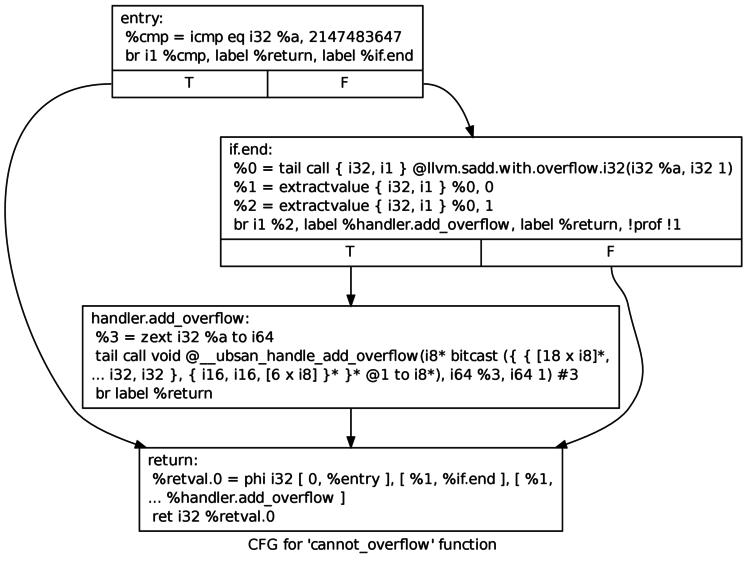
To characterize LLVM’s missing optimization in terms of the two-part model from the top of this piece, the optimizable situation is “an add-with-overflow instruction can be shown to never signal an overflow” and the replacement code is “regular add instruction” (getting rid of the call to the overflow handler is a separate optimization whose situation is “code that can be shown to not execute” and whose replacement code is “nothing”).

Should we conclude that LLVM isn’t very bright at optimizing integer expressions? No, and in fact that kind of generalization is seldom useful when talking about compiler optimizations — the devil is in the details. For example, let’s try an open-coded version of the overflow check:

static int safe_int_add (int a, int b)
{
  assert (!(b > 0 && a > INT_MAX-b));
  assert (!(b < 0 && a < INT_MIN-b));
  return a+b;
}

int cannot_overflow_2 (int a)
{
  if (a==INT_MAX) return 0;
  return safe_int_add (a, 1);
}

In this case, LLVM produces the ideal output. On the other hand, if we modify this code in a trivial way, LLVM cannot optimize away the assertions:

int cannot_overflow_3 (int a)
{
  if (a==INT_MAX) return 0;
  return safe_int_add (1, a);
}

Switching gears slightly, let’s take a quick look at GCC 4.8.1. It is unable to remove integer overflow checks inserted by its -ftrapv logic. It is, on the other hand, able to fully optimize both cannot_overflow_2() and cannot_overflow_3().

What’s the point? The point is that making a smart compiler is a years-long process of teaching it optimizations. This teaching process is very fine-grained. For example, we just saw that LLVM can emit good code for cannot_overflow_2() but not for the nearly-identical cannot_overflow_3(). To fix this, one or more LLVM passes need to be modified, an error prone process requiring the attention of a smart, experienced, expensive, and probably overworked compiler engineer. A totally different set of changes will be necessary to optimize the original cannot_overflow(). Wouldn’t it be nice if there was a better way to make a compiler smarter, freeing up our engineer to go implement C++14 or something?

Superoptimizers

Instead of relying on a human, a superoptimizer uses search-based techniques to find short, nearly-optimal code sequences. Since the original 1987 paper there have been several more papers; my favorite one is the peephole superoptimizer from 2006. For a number of years I’ve thought that LLVM would benefit from a peephole superoptimizer that operates on the IR.

Lately I’ve been thinking it might be time to actually work on this project. The thing that pushed me over the edge was a series of conversations with Xi Wang, whose excellent Stack tool already knows how to turn LLVM into an SMT instance so that a solver can answer questions about the LLVM code. For the purposes of a superoptimizer, we need the solver to prove equivalence between some LLVM IR found in a program and a smaller or faster piece of IR that we’d like to replace it with. As you can see in this file, the semantic gap between LLVM IR and a modern bitvector-aware SMT solver is small.

Before getting into the details, we need to look at this excellent work on superoptimizing LLVM IR, which contains two ideas not seen (that I know of) in previous superoptimizers. First, it works on a DAG of instructions instead of a linear sequence. Second, it exploits knowledge of undefined behaviors. On the other hand, this work has a few limitations that need to be fixed up. First, it doesn’t always come up with correct transformations. This issue is relatively easy to address via SMT solver. Second, its purpose is to feed ideas to a human who then adds some patterns to a compiler pass such as the instruction combiner. While manual implementation is pragmatic in the short run, I am guessing it is tedious and error prone and unnecessary, especially as the size of the replaced pieces of LLVM code grows.

Although I am writing up this blog post myself, there’s plenty of stuff here that came out of conversations with Xi Wang and Duncan Sands. Also both of them gave me feedback on drafts of this piece. In fact Duncan gave me so much feedback that I had to go rewrite several sections.

LLVM Superoptimizer Design Sketch

We’ve already seen that a compiler optimization needs to recognize optimizable code and replace it with better but functionally equivalent code. A third requirement is that it does these things very rapidly. Let’s look at how this might work for LLVM.

To find candidates for optimization, we’ll start with a largish collection of optimized LLVM IR and harvest every DAG of eligible instructions up to some size limit. At first, only ALU instructions will be eligible for superoptimization but I would expect we can handle memory operations, local control flow, and vectors without too much trouble. Floating point code and loops are more challenging. Here’s the documentation for LLVM IR in case you have not looked at it lately.

To suppress DAGs that differ only in irrelevant details, we need a canonicalization pass. Then, for each canonical DAG, our goal is to find a cheaper DAG that is functionally equivalent. This is expensive; not only will we need to do it offline, but probably we’ll also want to spread the work across a cluster. The method is to exhaustively enumerate canonical DAGs of LLVM code up to some smaller maximum size than we used in the harvesting phase. Next we need to answer the question: which of the enumerated DAGs are functionally equivalent to DAGs that we harvested? The technique from the 2006 superoptimizer was to use a few test vectors to rapidly rule out a large fraction of inequivalent code sequences and then to use a solver to soundly rule out the rest. The same idea will work here.

So far we’ve burned a lot of CPU time finding DAGs of LLVM instructions that can be replaced by cheaper instructions. The next problem is to make these transformations available at compile time without slowing down the compiler too much. We’ll need to rapidly identify qualifying DAGs in a file being optimized, canonicalize them, and rewrite them. Some sort of hashing scheme sounds like the way to go. Duncan suggests that we can use the superoptimizer itself to generate a fast canonicalizer — this would be cool.

In summary, we have the superoptimizer itself, which is slow. Most people won’t want to run it, but large organizations with significant compute resources might want to do so. We also have an LLVM pass that optimizes code using pre-computed optimizations that are generated automatically and proved correct by an SMT solver.

Improvements

Here are some ideas that are a bit more speculative.

Exploiting dataflow facts. One of the things I’m most excited to try out is optimizing each DAG in the context of a collection of dataflow facts such as “incoming variable x is a non-negative multiple of 4” and “incoming pointers p and q are not aliases.” I see this as a solid workaround for one of the main shortcomings of a peephole superoptimizer, which is that it myopically considers only a small amount of code at a time. Dataflow facts will support some action at a distance. Although constraints on inputs to a DAG — “incoming variable z is odd” or whatever — seem the most straightforward, I believe we can also exploit anti-constraints on outgoing values, such as “outgoing variable w is a don’t-care unless it is in the range [0..9].” The latter would happen, for example, if w was about to be used as an index into an array containing 10 values. It goes without saying that this kind of evil exploitation of undefined behavior should be optional and only makes sense when used in combination with UBSan-based testing.

Something that will happen at optimization time is that we’ll have a DAG in the code being optimized whose shape matches a DAG from the optimization database but the associated dataflow information doesn’t quite match up. I believe this is easy to deal with: we can perform the substitution if the dataflow information in the code being optimized is stronger than the dataflow information in the optimization database. For example, if we have a DAG where incoming value x>10, we can apply an optimization derived for the weaker condition x>0 but not the stronger condition x>20.

The problem with exploiting dataflow facts is that it makes every part of the superoptimizer more complicated. We’ll need to carefully consider what kind of dataflow information can actually give the superoptimizer good leverage. I’ve been reading passes like value tracking which seem to provide pretty much just what we want.

Avoiding the DAG enumeration step. Enumerating and testing candidate DAGs is inelegant. Wouldn’t it be nice to avoid this? The Denali and Denali-2 superoptimizers were based on the idea that a SAT solver could be used to directly synthesize an optimal instruction sequence matching a specification. The papers did not provide a lot of evidence that this technique worked, but what if Denali was simply ahead of its time? Improvements in SAT/SMT solvers and in processing power over the last decade may have made this technique, or a closely related one, into a realistic proposition.

Another reason to prefer synthesis vs. enumeration is that an enumeration-based approach can’t do much with constants: there are too many choices. This means that our superoptimizer is not going to discover awesome tricks like the fast inverse square root (which is an approximation, so it would fail the equivalence check, but you get the idea).

Better cost functions. Estimating the execution cost of a DAG of LLVM instructions is not totally straightforward since — despite the name — the IR is pretty high-level (it’s not like estimating the execution cost of actual instructions is easy either, on a modern processor). We can imagine estimating costs in simple, hacky ways such as counting instructions or measuring the longest path through the DAG. On the other hand, it may be worthwhile to do something more accurate such as compiling some DAGs to machine code, measuring their execution costs on some test vectors, and then using the resulting data to fit a cost model. Pluggable cost functions will make it easy to optimize for code size instead of speed — something compilers today are not particularly good at.

Duncan guesses that “number of instructions” is the only cost function that we’ll need, but I’m not so sure. Do we really want the superoptimizer to replace a shift and add with a multiply?

Optimizing entire loops. Although any superoptimizer can improve code inside of loops, I don’t know of any superoptimizer that targets code containing loops. There seem to be two obstacles. First, the search space may become problematically large. Second, the straightforward approach to encoding a loop in SMT — to unroll it a few times — is unsound. Can I use an SMT solver to prove equivalence of two loops with unknown numbers of iterations? I feel like I’ve read papers that discuss how to do this but I couldn’t find them just now — references would be appreciated.

Generalizing optimizations. Duncan’s superoptimizer worked in absence of LLVM type information, so it would derive a single rule permitting us to replace, for example, y-(x+y) with -x regardless of the (common) width of x and y. The superoptimizer that I have outlined will run into a bit of a rule explosion because it will derive a separate optimization for each width. Although the LLVM code that I have looked at is dominated by values of the obvious widths (1, 8, 16, 32, 64, 128), the rule explosion may become a serious problem when we try to take dataflow information into account. A fun piece of research would be make a superoptimizer that generalizes optimizations on its own. This might be done by attempting to generalize each optimization as it is derived or perhaps it should be done after the fact by running a generalization pass over the database of derived optimizations, looking for a collection of transformations that can be subsumed by a single more general rule. In summary, the performance and efficacy of our optimizer will be best if we generate broadly-applicable optimizations whenever possible and narrowly-applicable optimizations whenever necessary.

Integration with LLVM backends. An IR-only superoptimizer is always going to miss optimizations that exploit hardware features that are invisible at the LLVM level. For example, since LLVM has no rotate instruction, the kinds of optimizations discussed here are out of reach. This is an acceptable tradeoff, but on the other hand exploiting the detailed semantics of quirky instructions is an area where we would expect a superoptimizer to excel. Can our LLVM->LLVM superoptimizer be extended so that it helps with backend tasks in addition to optimizing IR, or is that the job of a completely separate superoptimizer? I do not know yet, but I do know that a purely post-pass superoptimizer (the 2006 peephole superoptimizer is an example of such a tool) is problematic because it is going to be difficult to make it aware of the concurrency model. In other words, it’s going to try to optimize away memory references that are used to communicate with other threads, with hardware devices, etc.

Outcomes

What outcomes might we expect if this work is successful?

Novel optimizations on real code. You can tell I’m not a real compiler person because I don’t care about making SPEC faster. That dusty pile of crap runs as fast as it’s ever going to run, as far as I’m concerned. On the other hand, there is almost certainly interesting idiomatic code coming out of Emscripten and GHC that LLVM can’t yet optimize fully. Similarly, as I showed at the top of this piece, when we turn on integer overflow checking in Clang, the generated code has plenty of room for improvement. The holy grail of superoptimization is automated discovery and application of tricks like the ones we read in Hacker’s Delight.

Undefined programs implode. Not too long ago I wrote a modest proposal about aggressive exploitation of undefined behavior. Just to be clear, I was not being entirely serious. Well, guess what? An UB-aware superoptimizer is going to smash undefined programs in more or less the way that I described. Obviously I have mixed feelings about this, but my belief is that as long as every undefined behavior that is exploited by the superoptimizer has a corresponding UBSan check, this might be a reasonable tradeoff.

Existing compiler passes are subsumed. Ideally, we point a superoptimizer at unoptimized LLVM code and once a fixpoint is reached, the code is at least as good as what the LLVM optimizers would have produced. I don’t expect this to happen, but on the other hand the 2006 superoptimizer was able to take a small function in unoptimized x86 and turn it into roughly the equivalent of gcc -O2 output. The intriguing possibility here is that compiler internals, which have been growing more complex for decades, could become simpler by relying on a superoptimizer for some classes of transformations. I think we can hope to replace parts of the instruction combiner, which was one of the most fruitful sources of wrong-code bugs that we found after pointing Csmith at LLVM.

We pave the way for more ambitious tools. A while ago I wrote that CompCert needs a superoptimizer. This is still true. I’m not going to work on it, but I would hope that techniques and lessons gained from one superoptimizer will help us create other ones.

Conclusions

Superoptimizer results have already percolated into LLVM and GCC by suggesting missed optimizations. I think it’s time for this technology to play a more direct role. A realistic superoptimizer, once set in motion, will naturally absorb improvements in SMT solving and in compute power. For example, if we can harvest IR DAGs up to size 10 this year, it might be 12 next year. If this idea works out, it leaves compiler developers with more time to focus on other tasks.

Updates from March 4:

• The title of this piece says “let’s work” but the subsequent paragraph explaining this got lost during some revision. What I mean is that I think it would be a good idea to work on this project in an open source fashion. My group has already had very good experiences with Csmith and C-Reduce as open source tools. One part of the equation that complicates things is that as a researcher, I will need to publish papers based on this work. The right solution, I believe, is to give everyone who contributed to the work being described in a paper the opportunity to be a co-author.

• At ASPLOS yesterday I had a good talk with Santosh Nagarakatte; his Verified LLVM work is related to this post, it would be cool to make these projects work together somehow.

• I also talked to Vikram Adve; his intuition is that a superoptimizer has more to contribute to the backend than the middle end. This may end up being the case, but let’s review the rationale for a middle-end superoptimizer. First, it is wrong to generate dead code in the backend, and the superoptimizer will be doing that sometimes — as well as generating other kinds of code that wants to be further optimized by other passes. Second, by operating only on the IR, we gain all sorts of simplicity that will make it easier to pursue more ambitious projects such as exploiting dataflow information, synthesizing optimal IR, etc. As I said above, a backend superoptimizer is definitely also desirable.

And thanks for all the good comments!