At some point we’ll be able to run a computer simulation that contains self-aware entities. In this piece I’m not going to worry about little details such as how to tell if a simulated entity is self-aware or whether it’s even possible to run such a simulation. The goal, rather, is to look into some philosophical problems posed by simulations.
A computer simulation takes a model in some initial configuration and evolves the state of the model through repeated programmatic application of rules. Usually we run a simulation in order to better understand the dynamics of some process that is hard to study analytically or experimentally. The straightforward way to implement a simulator is to represent the system state in some explicit fashion, and to explicitly run the rule set on every element of the state at every time step. It seems clear that if our simulation includes a self-aware entity, this sort of execution is sufficient to breathe life into the entity. But what about other implementation options?
First, our simulator might be mechanically optimized by a compiler or similar tool that would combine rules or elide rules in certain situations. For example, if the simulation state contains a large area of empty cells, the optimizer might be able to avoid running the rule set at all in that part of the space. Can the entity being simulated “feel” or otherwise notice the compiler optimizations? No — as long as the compiler is correct, its transformations are semantics preserving: they do not affect the computation being performed. Of course a suitable definition of “do not effect” has to be formulated; typically it involves defining a set of externally visible program behaviors such as interactions with the operating system and I/O devices.
 |
Compiler optimizations, however, are not the end of the story — algorithmic optimizations can be much more aggressive. I’ll use Conway’s Game of Life as the example. First a bit of background: Life is a two-state, rectangular cellular automaton governed by these rules (here I’m quoting from Wikipedia):
- Any live cell with fewer than two live neighbors dies, as if caused by under-population.
- Any live cell with two or three live neighbors lives on to the next generation.
- Any live cell with more than three live neighbors dies, as if by overcrowding.
- Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
Life has been shown to be Turing complete, so clearly self-aware entities can be encoded in a Life configuration if they can be algorithmically simulated at all. A straightforward implementation of Life maintains two copies of the Life grid, using one bit per cell; at every step the rules are applied to every cell of the old grid, with the results being placed into the new grid. At this point the old and new grids are swapped and the simulation continues.
Hashlife is a clever optimization that treats the Life grid as a hierarchy of quadtrees. By observing that the maximum speed of signal propagation in a Life configuration is one cell per step, it becomes possible to evolve squares of the Life grid multiple steps into the future using hash codes. Hashlife is amazing to watch: it starts out slow but as the hashtable fills up, it suddenly “explodes” into exponential progress. I recommend Golly. Hashlife is one of my ten all-time favorite algorithms.
The weird thing about Hashlife is that time progresses at different rates at different parts of the grid. In fact, two cells that are separated by distance n can be up to n time steps apart. Another interesting thing is that chunks of the grid may evolve forward by many steps without the intermediate steps being computed explicitly. Again we ask: can self-aware Life entities “feel” the optimization? It would seem that they cannot: since the rules of their universe are not being changed, their subjective experience cannot change. (The Hashlife example is from Hans Moravec’s Mind Children.)
If Hashlife is a viable technology for simulating self-aware entities, can we extend its logic to simply replace the initial simulation state with the final state, in cases where we can predict the final state? This would be possible for simulated universes that provably wind down to a known steady state, for example due to some analogue of the second law of thermodynamics. The difference between Hashlife and “single simulation step to heat death” is only a matter of degree. Does this fact invalidate Hashlife as a suitable algorithm for simulating self-aware creatures, or does it imply that we don’t actually need to run simulations? Perhaps to make a simulation “real” it is only necessary to set up its initial conditions. (Greg Egan’s Permutation City is about this idea.)
Aside: Why don’t we have processor simulators based on Hashlife-like ideas? Although ISA-level simulators do not have the kind of maximum speed of signal propagation seen in cellular automata, the programs they run do have strong spatial and temporal locality, and I bet it’s exploitable in some cases. I’ve spent long hours waiting for simulations of large collections of simple processors, daydreaming about all of the stupid redundancy that could be eliminated by a memoized algorithm.
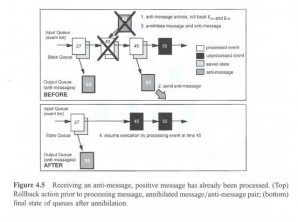 |
Techniques like Hashlife only go so far; to get more speedup we’ll need parallelism. In this scenario, the simulation grid is partitioned across processors, with inter-processor communication being required at the boundaries. An unfortunate thing about a straightforward implementation of this kind of simulation is that processors execute basically in lock step: at least at the fringes of the grid, no processor can be very far ahead of its neighbors. The synchronization required to keep processors in lock step typically causes slowdown. Another ingenious simulation speedup (developed, as it happens, around the same time as Hashlife) is Time Warp, which relaxes the synchronization requirements, permitting a processor to run well ahead of its neighbors. This opens up the possibility that a processor will at some point receive a message that violates causality: it needs to be executed in the past. Clearly this is a problem. The solution is to roll back the simulation state to the time of the message and resume execution from there. If rollbacks are infrequent, overall performance may increase due to improved asynchrony. This is a form of optimistic concurrency and it can be shown to preserve the meaning of a simulation in the sense that the Time Warp implementation must always return the same final answer as the non-optimistic implementation.
Time Warp places no inherent limit on the amount of speculative execution that may occur — it is possible that years of simulation time would need to be rolled back by the arrival of some long-delayed message. Now we have the possibility that a painful injury done to a simulated entity will happen two or more times due to poorly-timed rollbacks. Even weirder, an entity might be dead for some time before being brought back to life by a rollback. Depending on the content of the message from the past, it might not even die during re-execution. Do we care about this? Is speculative execution amoral? If we suppress time warping due to moral considerations, must we also turn off processor-level speculative execution? What if all of human history is a speculative mistake that will be wiped out when the giant processor in the sky rolls back to some prehistoric time in order to take an Earth-sterilizing gamma ray burst into account? Or perhaps, on the other hand, these speculative executions don’t lead to “real experiences” for the simulated entities. But why not?
The Hashlife and Time Warp ideas, pushed just a little, lead to very odd implications for the subjective experience of simulated beings. In question form:
First, what kind of simulation is required to generate self-awareness? Does a straightforward simulator with an explicit grid and explicit rule applications do it? Does Hashlife? Is self-awareness generated by taking the entire simulation from initial state to heat death in a single step? Second, what is the effect of speculative execution on self-aware entities? Do speculative birth and death, pain and love count as true experiences, or are they somehow invalid?
These questions are difficult — or silly — enough that I have to conclude that there’s something fundamentally fishy about the entire idea of simulating self aware entities. (Update: Someone told me about the Sorites paradox, which captures the problem here nicely.) Let’s look at a few possibilities for what might have gone wrong:
- The concept of self-awareness is ill-defined or nonsensical at a technical level.
- It is not possible to simulate self-aware entities because they rely on quantum effects that are beyond our abilities to simulate.
- It is not possible to simulate self-aware entities because self-awareness comes from souls that are handed out by God.
- We lack programming languages and compilers that consider self-awareness to be a legitimate side-effect that must not be optimized away.
- With respect to a simulation large enough to contain self-aware entities, effects due to state hashing and speculation are microscopic — much like quantum effects are to us — and their effects are necessarily insignificant at the macroscopic level.
- All mathematically describable systems already exist in a physical sense (see Max Tegmark’s The Mathematical Universe — the source of the title of this piece) and therefore the fire, as it were, has already been breathed into all possible world-describing equations. Thus, while simulations give us windows into these other worlds, they have no bearing on the subjective experiences of the entities in those worlds.
The last possibility is perhaps a bit radical but it’s the one that I prefer: first because I don’t buy any of the others, and second because it avoids the problem of figuring out why the equations governing our own universe are special — by declaring that they are not. It also makes simulation arguments moot. One interesting feature of the mathematical universe is that even the very strange universes, such as those corresponding to simulations where we inject burning bushes and whatnot, have a true physical existence. However, the physical laws governing these would seem to be seriously baroque and therefore (assuming that the multiverse discourages complexity in some appropriate fashion) these universes are fundamentally less common than those with more tractable laws.
22 responses to “Does a Simulation Really Need to Be Run?”
Mass murder by pressing a button.
IT should be forbidden.
Running a computer without a UPS? Negligent homicide.
Accepting Tegmark’s Level 4 multiverse is one heck of a bullet to bite!
> With respect to a simulation large enough to contain self-aware entities, effects due to state hashing and speculation are microscopic — much like quantum effects are to us — and their effects are necessarily insignificant at the macroscopic level.
I like this one. We can already do very strange things as the implementation. We can have processors made out of Toffoli or Fredkin gates, or using only a single instruction like subtract-one-and-branch-if-negative, or implementations of FRACTRAN; we can use error-correcting codes to split files up into 9 different files such that no file conveys any information about the original but 3 let you recreate the original; we can have shared multiparty computations (from cryptography) where the same is true but of the computation rather than data; or heck, homomorphic encryption is so weird it doesn’t need explanation.
But the results are still ordinary, still add up to what we want them to add up to. If this is so about a small combination of logic gates (ordinary programs like `ls`), then why would it break down when scaled up to programs as large and complicated as minds?
As long as the computation is isomorphic, if the same domain maps onto the same range, what’s the problem? Shuttling electrons around silicon is pretty strange when you think about it; there’s nothing more ‘natural’ about x86-64 than about all the other examples. (Chemistry and biology are even more bizarre from the point of view of implementing a mind, I should mention. All those crazy nigh-arbitrary chemical reactions, enzyme functions, and loops and hierarchies of compounds and organelles? Only something like evolution could get a mind out of that kind of mess of a substrate.)
I go with #5, because I agree with Hofstadter’s argument that (in a really tiny nutshell) consciousness is a system which self-referentially maintains models of itself. These models are implemented using the underlying system, but are not modeling that system.
Thus any discontinuities in the underlying system are in a separate order, much like the shuffling of data in a CPU vs. the algorithm it’s running, or better yet, the relationship of ink lettering with the story of the book.
#6, absolutely! At some point in your argument I began to wonder why exactly you saw a problem, and realized immediately you weren’t thinking in terms of the Platonic reality of mathematics. I do think there are other ways of looking at the problem, though; for example i’ve never thought of Hashlife as genuinely simulating Life, because it skips steps. I think you could look at simulation in terms of what answers the program gives you back and some of the problems go away.
For example, if the simulation actually gives you back information about someone’s hypothetical death, or the information could theoretically be retrieved, then yes, it just got simulated. If on the other hand, a simulation skips straight to heat death, then it actually doesn’t allow us to obtain information about what happened in between.
I don’t think #5 is plausible, because there could always be large-scale effects like an asteroid coming out of nowhere. But my overall impression of that list of possibilities is that it is inelegant and therefore can’t be exhaustive. If it were more clearly exhaustive I think this would be a great argument for mathematical realism.
Answer #6, even if we accept it as true, tells us absolutely nothing about whether a simulation is self-aware. Do you understand this? It’s like if I punch you in the face, and I want to know whether it hurt you, and you say “The multiverse contains all possible punches that hurt.” So what? I want to know if the punch that I just threw, here and now, made an impact.
Gwern, I agree, all of our substrates are pretty bizarre when you think about them!
Dranorter, I don’t really believe that observing a simulation is what makes it real, but that definitely belongs on the list as a possibility.
I agree, a more exhaustive list would be great. Please help :).
This is the exact problem raised in science fiction novel “Permutation City”… Greg Egan is not my favorite writer, but he is really original, thanks to his math background and a unique dedication to rational and scientific thinking.
The key question for me is how important memory is to self-awareness. Would a self-aware glider “remember” being in a previous location even if it had just come into existence as a result of a catastrophic event such as a rollback?
Richardc, all memory has to be encoded in the simulation state, so yes — a self-aware entity would definitely have its full memory following a rollback.
Similarly, neither of us can prove that the universe wasn’t created 15 minutes ago with everyone having been given a full set of memories.
This has already been determined at some point with mathematical certainty (I think it’s gone over in Wolfram):
There are discrete dynamical systems which are turing complete and you cannot ‘skip’ ahead. You must run the simulation.
Memory is important to self-awareness. If you consider the statement “I think there I am”, if you forgot that you thought about “I think” then would you really say “I am”?
I have always had an intuitive thought that a simulation turns out to be a “brute-force” enumeration of the simulation space. Some simulations are more “brute” than others. All in all, this means that a simulation eventually converges on the syntactic and (to be argued) semantic nature of the physical reality.
It seems there is an unexplored mash-up of scientific research in the fields of computational complexity theory, statistical mechanics, linguistics, graph theory, fractal algebra and geometry. At least this is a good starting point.
I love how you sneak the word “amoral” in your post without providing any rigorous definition.
I’m just going to reword this a bit.
Is time necessary for being to exist?
When we say that conway’s game of life starts at an initial 2D condition, and arrives at a 2D final answer, we leave the middle implicit. But really, the initial 2D conditions + the processing rules = a 3D space.
Ok, so using a 3D space, we can describe time in the context of game, by redefining time as just a dimension of space, but is that enough?
Or, does there exist a ‘true’ time. Do we need an observer, or a simulator, that exists in ‘true’ time, to ‘lend’ their time to this space, for being to arise? What happens if their ‘true’ time maps non-linearly to the game’s time?
#6 says that ‘true’ time is not necessary, and even more strongly, that it does not exist.
Personally, I’m not opposed to #6. But it does mean there is no difference between possibility and reality. For example, it’d be interesting to know what limits exist that would make it necessary to discourage complex physical laws that would lead to burning bushes. I would think a brute force inventory of all possible worlds would lead to complex worlds far out-numbering simple ones.
Interesting points.
Now, if I were running a simulation of this world I would not bother to simulate every possible particle — unless ‘somebody’ is observing it. That is, I’d run optimized code that cuts corner (similar to your ‘heat death’) only when the results — and not the process itself — matters.
How do I know if somebody is observing? I don’t. That’s why I would rollback and run the simulation again with the appropriate level of detail.
Since we’re stretching metaphors, take a flocking simulation: there’s no need to render every feather nor to model every particle in every member of the flock. You use general rules that describe well the overall behaviour. If you notice that one Jonathan Livingston, seagull is paying attention to the quantum particles, well, you just rollback and re-run the simulation with all the details that the observer can handle. At some point your simulated entities will have to stop (*cough* Planck length *cough*) at the basic time interval you decided.
Ah, lazy weekends 🙂
Links for the curious! You already brought up Permutation City, which contains some pretty great (and fun-to-read!) thinking on this subject. I recommend the short story Transition Dreams, also by Greg Egan. It’s a rather scary extrapolation of what happens if conscious experience arises from any physical process encoding it. Eliezer Yudkowsky’s blog post Beyond the Reach of God is also somewhat relevant, although it’s really more about emotionally handling the idea of living in a reductionistic universe, but it does brings up the question of whether it matters morally whether you run the simulation or not.
If the simulation is deterministic, of course it doesn’t matter whether you actually run it or not. It can only proceed through exactly one sequence of states, entirely determined by the initial state.
Even if its non-deterministic, as long as you are simulating a closed system that is isolated from the outside (“real”) world, then I don’t think it matters whether you run the simulation zero times, one time, N times, partially or repeatedly, etc.
Still, for a non-deterministic system its not 100% clear to me whether you can actually simulate a “complete” system without some of the “real” world state “leaking into it” in some fashion. (e.g. are the laws of probability in the simulation affected in some way by how you make the non-deterministic choices while running it? If you add a bias of some sort in your random number source, does that actually change the system being simulated into a different system?)
Moo, I don’t think non-determinism adds anything fundamental to the picture. A non-deterministic simulation can be seen as a large family of deterministic simulations, each corresponding to some choices of branches.
I’m a fan of the many-worlds interpretation of quantum physics. However, I see the multiverse as a giant NFA (nondeterministic finite automaton). …at least, I hope its finite! Hmm. Any given snapshot of the universe, is a state somewhere in this giant NFA. So the existence of “many parallel universes” just looks like “many different NFA states” to me. Obviously with this view of things, there’s no need to actually simulate the universe. We perceive ourselves as existing and we perceive a forward flow of time, and remember things we perceived during earlier states… but all of this is captured as part of the entire-universe-state snapshot that is a state in the NFA.
You might want to reconsider #5 after watching this: http://www.ted.com/talks/aaron_o_connell_making_sense_of_a_visible_quantum_object.html