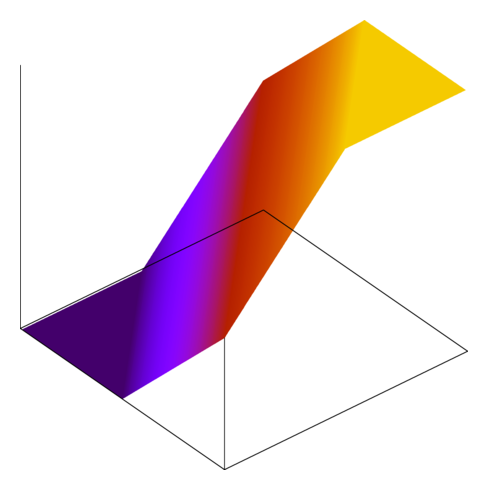
Testing code is fun and hard and looking at the problem in different ways is always good. Here’s a picture representing the behavior of a saturating subtraction operation, where the horizontal axes represent the inputs and the output is vertical:
And here are some of the functions handed in by my students in the fall:
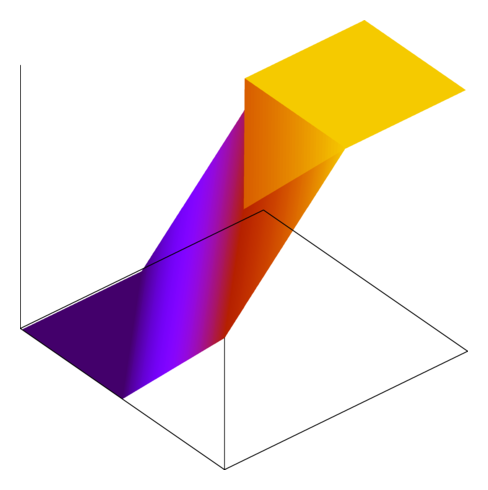

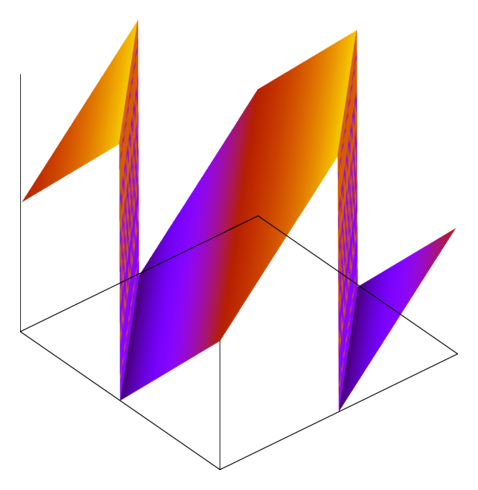
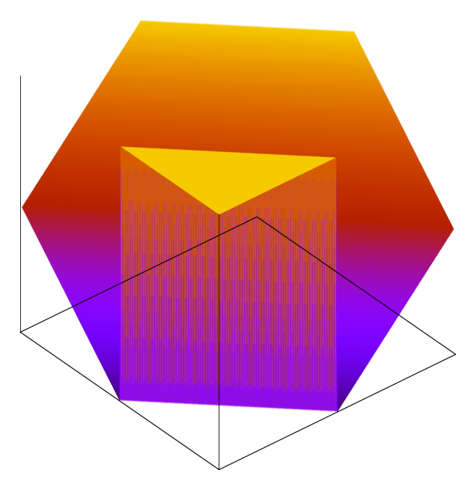

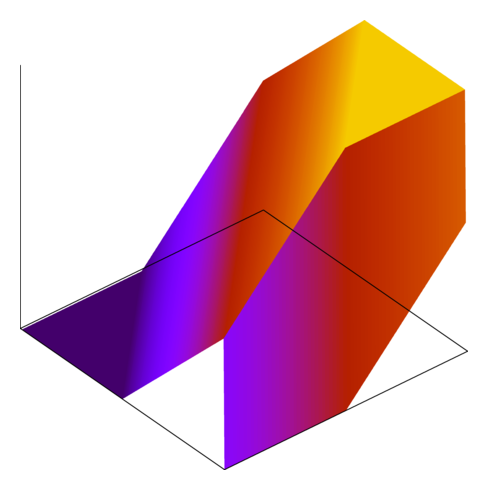


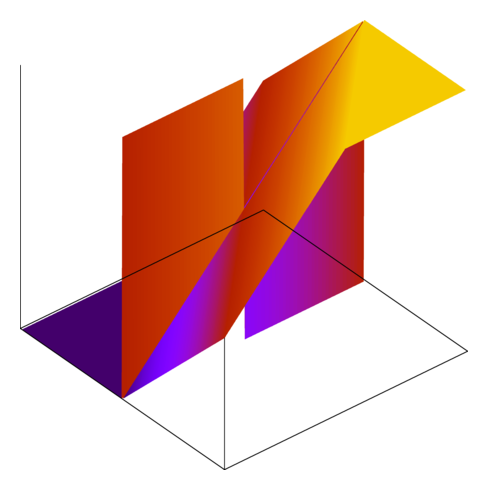
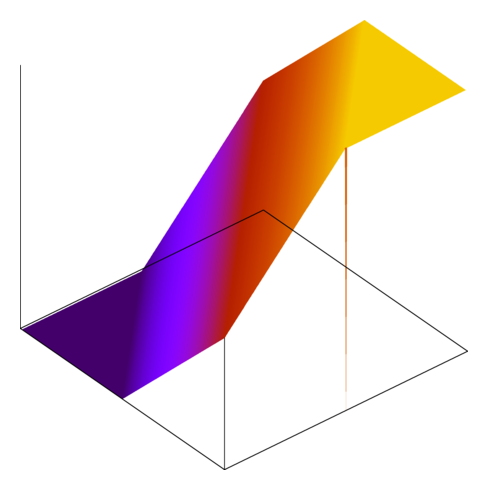
The last one represents one of the most common failure modes: failing to account for the asymmetry where INT_MIN has no additive inverse. The thing that I like about these images is how glaringly obvious the bugs are.
Hey, who knew Gnuplot could do animated gifs now? I guess old dogs can learn new tricks.

(Note: I posted some of these a few years ago, but I like the pictures so much I wanted to do it again.)
7 responses to “Testing with Pictures”
I’m wondering what would happen if you taught them about the pictures before the assignment.
That is, even if you didn’t show them the picture of the right function, it’s “obvious” which properties of arithmetic are being violated with the discontinuities and wrong slopes.
Carlos, I intended to do that but just ran out of time. I assume that — as you say — the bugs would have been pretty easy to spot.
I followed the links to the description of your saturated arithmetic assignment. I suspect your “Big hint” should refer to trying to implement sat_signed_sub(a, b) as sat_signed_add (a, -b). I also have to admit that I see no way to determine the signed integer bounds in the face of those arbitrary typedefs. (For unsigned types, 0 and ((unsigned_int_type) -1) suffice.) Are students allowed to set those bounds along with the typedefs?
Yup I have to agree with Joshua Green there and actually posted a question on Stackoverflow (http://stackoverflow.com/questions/27786487/maximum-value-of-typedefed-signed-type) about it. The conclusion there seems to be that you can only get the bounds of a signed integer by relying on implementation defined behavior. Also I doubt that the compiler would recognize the pattern and avoid generating code.
Hi voo and Joshua, students are permitted to assume two’s complement for signed integers, which makes it easy to compute the min/max signed values. The resulting code is not technically portable, but then again no C code is technically portable.
I do occasionally see a few solutions that seem to be truly portable C code, but I have no good way to test them since I lack one’s complement and sign-magnitude compilers.
Reminds me of http://cr.yp.to/mac/variability1.html