(See this blog post for a short introduction to synthesis, or this paper for a long one.)

In this piece I want to discuss an aspect of program synthesis that sounds like it should be easy, but isn’t: synthesizing constant values. For example, consider trying to synthesize an optimized x86-64 implementation of this code:

long foo(long x) {
    return x / 52223;
}

The desired output is something like:

foo(long):
        movabs  rdx, -6872094784941870951
        mov     rax, rdi
        imul    rdx
        lea     rax, [rdx+rdi]
        sar     rdi, 63
        sar     rax, 15
        sub     rax, rdi
        ret

Assume for a moment that we know that this sequence of instructions will work, and we only lack the specific constants:

foo(long):
        movabs  rdx, C1
        mov     rax, rdi
        imul    rdx
        lea     rax, [rdx+rdi]
        sar     rdi, C2
        sar     rax, C3
        sub     rax, rdi
        ret

We need to find a 64-bit constant and two 6-bit constants such that the assembly code returns the same result as the C code for every value of the function parameter. Of course there’s a well-known algorithm that GCC and LLVM use to compute these constants, but the synthesizer doesn’t have it: it must operate from first principles.

An even more difficult example is a 64-bit Hamming weight computation, where (assuming we don’t want to use vector instructions) we might hope to synthesize something like this:

popcount64(unsigned long):
        movabs  rdx, 6148914691236517205
        mov     rax, rdi
        shr     rax
        and     rax, rdx
        movabs  rdx, 3689348814741910323
        sub     rdi, rax
        mov     rax, rdi
        shr     rdi, 2
        and     rax, rdx
        and     rdi, rdx
        add     rdi, rax
        mov     rax, rdi
        shr     rax, 4
        add     rax, rdi
        movabs  rdi, 1085102592571150095
        and     rax, rdi
        movabs  rdi, 72340172838076673
        imul    rax, rdi
        shr     rax, 56
        ret

Again assuming that we know that this sequence of instructions will work, we still need to come up with 280 bits worth of constant values. One can imagine even more challenging problems where we want to synthesize an entire lookup table.

The running example I’ll use in this post is much easier:

uint32_t bar1(uint32_t x) {
  return ((x << 8) >> 16) << 8;
}

The code we want to synthesize is:

uint32_t bar2(uint32_t x) {
  return x & 0xffff00;
}

That is, we want to find C in this skeleton:

uint32_t bar3(uint32_t x) {
  return x & C;
}

Basic Constant Synthesis

We need to solve an “exists-forall” problem: does there exist a C such that the LHS (left-hand side, the original code) is equivalent to the RHS (right-hand side, the optimized code) for all values of x? In other words:

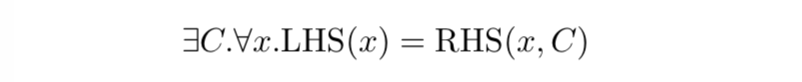
(Here we’ll play fast and loose with the fact that in the real world we check refinement instead of equivalence — this doesn’t matter for purposes of this post.)

The specific formula that we want an answer for is:

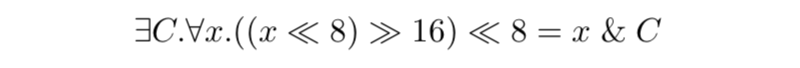
A SAT solver can natively solve either an exists query (this is the definition of SAT) or else a forall query (by seeing if there exists a solution to the negated proposition). But, by itself, a SAT solver cannot solve an exists-forall query in one go. An SMT solver, on the other hand, can natively attack an exists-forall query, but in practice we tend to get better results by doing our own quantifier elimination based only on SAT calls. First, we ask the solver if there exists a C and x that make the LHS and RHS equivalent. If not, synthesis fails. If so, we issue a second query to see if C works for all values of x. If so, synthesis succeeds. If not, we add a constraint that this value of C doesn’t work, and we start the process again. The problem is that each pair of queries only rules out a single choice for C, making this process equivalent, in the worst case, to exhaustive guessing, which we cannot do when C is wide. We need to do better.

Reducing the Number of Counterexamples using Specialization

Souper uses a technique that appears to be common knowledge among people who do this kind of work; unfortunately I don’t know where it was first published (Section 4.2 of this paper is one place it has appeared). The trick is simple: we choose a few values of x and use it to specialize both the LHS and RHS of the equation; you can think of this as borrowing some constraints from the forall phase and moving them into the exists phase (which becomes an “exists-forsome” query, if you will). In many cases this adds enough extra constraints that the solver can arrive at a workable constant within a few iterations. If we specialize x with 0 and -1 then in the general case we get:

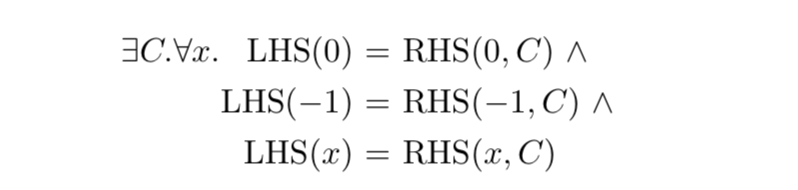
After constant folding, our running example becomes:

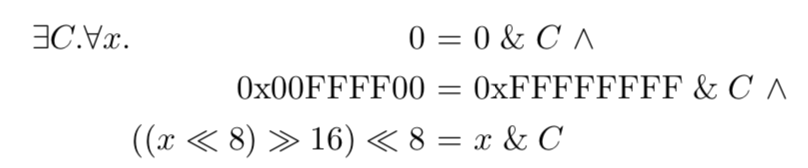
The first choice, 0, turns out to be an unlucky one: after further simplification it comes out to “0 = 0”, giving the solver no extra information. The second choice, on the other hand, is extremely lucky: it can be rewritten as “0x00FFFF00 = C” which simply hands us the answer. In most cases things won’t work out so nicely, but specializing the LHS and RHS with fixed inputs helps enormously in practice.

Some open questions remain: How many specific values should we try? How should these values be chosen? An obvious constraint is that the values chosen should be as different from each other as possible, though it isn’t clear what distance metric should be used. A related but less obvious criterion (this is Nuno Lopes’s idea, and we haven’t tried it out yet in Souper) is that the values should exercise as many different behaviors of each instruction as possible. For example, an addition instruction should have example inputs that overflow and also inputs that don’t. This requirement can be satisfied syntactically for instructions that are close to the inputs, but solver calls (or other symbolic methods) will be required to reach instructions that consume the outputs of other instructions. (In Souper’s case, solver calls are required anyway if there are any path conditions, which place arbitrary restrictions on the input space.) It also seems possible that we could tailor the input values to maximize how much of the RHS folds away (the LHS always folds completely down to a constant, of course).

Synthesis at Reduced Bitwidth

Instead of solving a difficult synthesis problem, we can instead solve a problem that is structurally identical, but uses narrower bitvectors (even two or three bits are often enough to capture the essence of a computation). This results in far better solver performance and, typically, a narrow synthesis result that does not contain constants will also work at the original, wider bitwidth (though obviously this needs to be verified by the solver). When the narrow result has constants, there’s a problem: we lack a principled method for deriving the wider constants from the narrow ones. One approach is to use heuristics. This paper suggests the following methods:

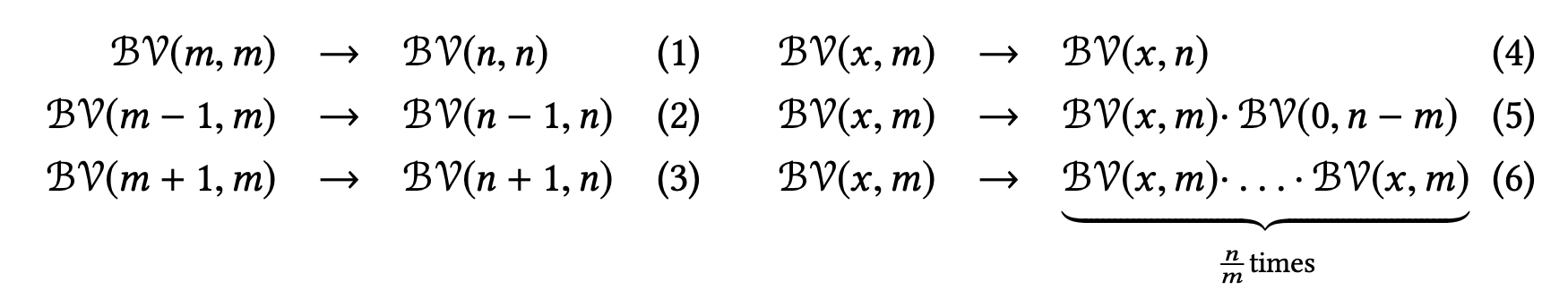
Here you should read BV(x,y) as “a bitvector of length y holding value x.” So, for example, rule 1 would extend an 8-bit variable containing 8 to a 16-bit variable containing 16. Rule 4 would extend an 8-bit variable containing 8 to a 16-bit variable containing 8. These seem reasonable, but notice that none of them would help with our running example.

In Souper we have the additional problem that the codes we’re trying to optimize usually contain constants, presenting us with a constant-narrowing problem that is analogous to the constant-widening problem that we just discussed, but worse because now any dodgy heuristics that we come up with are located in front of the expensive synthesis process instead of in back of it. It isn’t clear to us that there’s any satisfactory solution to this problem.

Getting More out of Counterexamples

In standard constant synthesis, each failed guess only adds the constraint that that particular constant doesn’t work — this fails to make much of a dent in an exponential search space. This paper and this one propose extracting additional information from each counterexample, cutting out a larger part of the search space. This also seems like an excellent direction.

Symbolic Constants

An alternate approach that avoids both narrowing and widening problems would be to treat constants symbolically. This, however, creates two new problems: deriving preconditions for optimizations and deriving functions to compute RHS constants in terms of elements of the LHS (constants, widths, etc.). It seems clear that in some cases this will be very difficult, for example imagine trying to derive, from first principles, the algorithm for computing the output constants for an arbitrary value of the LHS constant C:

long foo(long x) {
    return x / C;
}

Alive-Infer helps derive preconditions but it does not yet try to come up with the functions for computing constants in the synthesized output.

Since in some use cases (including my “destroy InstSimplify and InstCombine” dream) we want the generalized optimization anyway, this seems like a great direction for future work.

Conclusion

All of the techniques described in this post could be implemented inside the solver or outside it. Solvers like CVC4 already have sophisticated internal support for synthesis. The advantage of pushing more work into the solver is that it can exploit internal levers to guide the search, reuse data structures across synthesis iterations, and do other clever things that aren’t exposed by the solver’s API. The disadvantage is that we might have high-level information about the problem domain that is difficult to communicate effectively to the solver, that would help it do its job better.

In summary, constant synthesis is a hard problem that hasn’t received a lot of attention yet. My group is actively working on this and we have some ideas that aren’t mature enough to share yet. Please drop me a line if you know of any good techniques that I’ve missed here. Also, I’d be interested to hear from anyone working on benchmarks for constant synthesis.

Finally, tools such as Rosette and Sketch know how to synthesize constants.