[Also see Part 1 and Part 2 in this series.]
Let’s talk about these functions:
unsigned add(unsigned x) { return x + x; }
unsigned shift(unsigned x) { return x << 1; }
From the point of view of the C and C++ abstract machines, their behavior is equivalent: in a program you’re writing, you can always safely substitute add for shift, or shift for add.
If we compile them to LLVM IR with optimizations enabled, LLVM will canonicalize both functions to the version containing the shift operator. Although it might seem that this choice is an arbitrary one, it turns out there is a very real difference between these two functions:
define i32 @add(i32 %0) {
%2 = add i32 %0, %0
ret i32 %2
}
define i32 @shift(i32 %0) {
%2 = shl i32 %0, 1
ret i32 %2
}At the LLVM level, add can always be replaced by shift, but it is not generally safe to replace shift with add. (In these linked pages, I’ve renamed the functions to src and tgt so that Alive2 knows which way the transformation is supposed to go.)
To understand why add can be replaced by shift, but shift cannot be replaced by add, we need to know that these functions don’t have 232 possible input values, but rather 232+2. Analogously, an LLVM function taking an i1 (Boolean) argument has four possible input values, not the two you were probably expecting. These extra two values, undef and poison, cause a disproportionate amount of trouble because they follow different rules than regular values follow. This post won’t discuss poison further. Undef sort of models uninitialized storage: it can resolve to any value of its type. Unless we can specifically prove that an LLVM value, such as the input to a function, cannot be undef, we must assume that it might be undef. Many compiler bugs have been introduced because compiler developers either forgot about this possibility, or else failed to reason about it correctly.
Let’s look at some things you’re allowed to do with undef. You can leave it alone:

You can replace it with zero:

You can replace it with any number you choose:

You can replace it with the set of odd numbers:
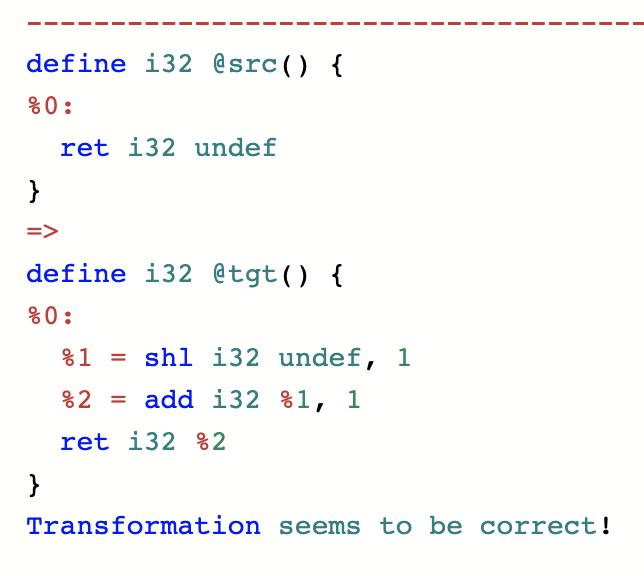
You can take a function that returns [0..15] and replace it by a function that returns [3..10]:

The common pattern here is that the new function returns a subset of the values returned by the old function. This is the essence of refinement, which is what every step of a correct compilation pipeline must do. (Though keep in mind that right now we’re looking at a particularly simple special case: a pure function that takes no arguments.) So what can’t you do with undef? This is easy: you can’t violate refinement. In other words, you can’t replace a (pure, zero-argument) function with a function that fails to return a subset of the values that is returned by the original one.
So, for example, you can’t take a function that returns [0..15] and replace it by a function that returns [9..16]:
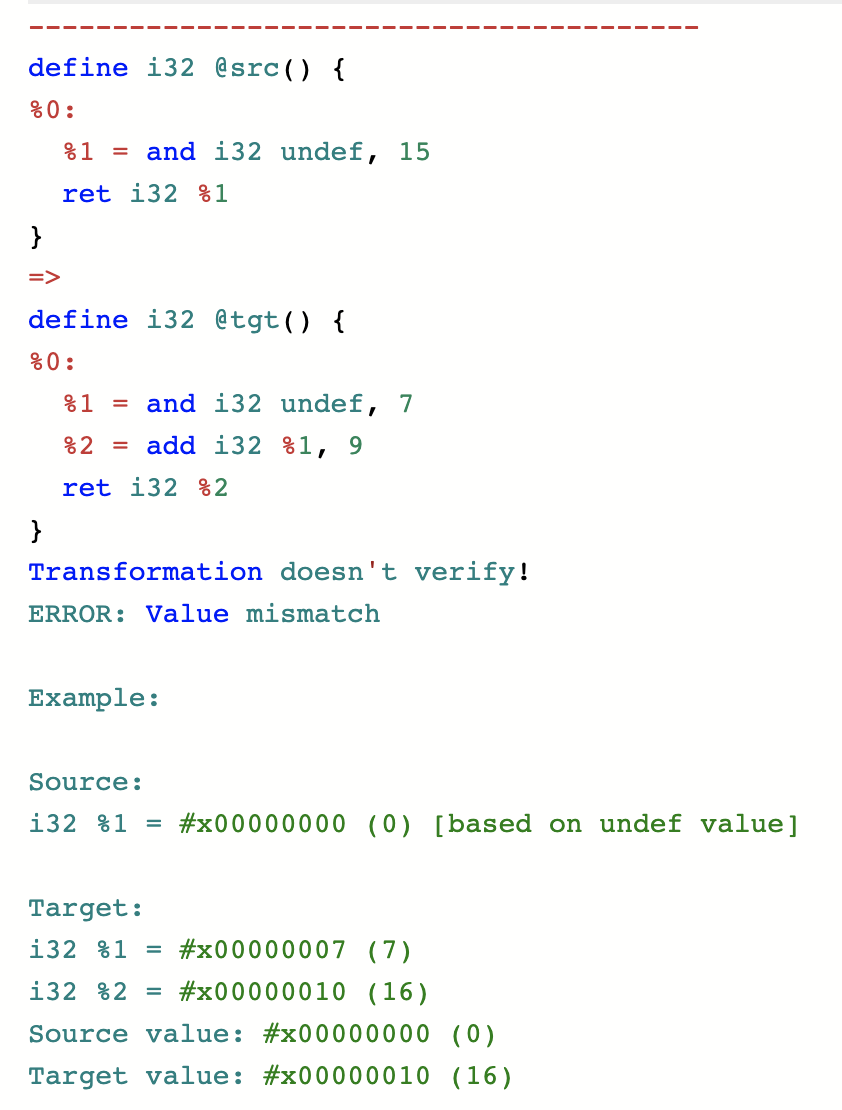
As we can see in the counterexample, Alive2 has correctly identified 16 as the problematic output. Returning [9..15] would have been fine, as would any other subset of [0..15].
When a function takes inputs, the refinement rule is: for every valuation of the inputs, the new function must return a subset of the values returned by the old function. Refinement gets more complicated for functions that touch memory; my colleagues Juneyoung and Nuno will cover that in a different post.
Now let’s return to the question from the top of this piece: why can we turn add into shift, but not shift into add? This is because every time an undef is used, the use can result in a different value (here “use” has a precise meaning from SSA). If undef is passed to the shift function, an arbitrary value is left-shifted by one position, resulting in an arbitrary even value being returned. On the other hand, the add function uses the undef value twice. When two different arbitrary values are added together, the result is an arbitrary value. This is a clear failure of refinement because the set of all 32-bit values fails to be a subset of the set of the even numbers in 0..232-1. Why was undef designed this way? It is to give the compiler maximum freedom when translating undef. If LLVM mandated that every use of an undef returned the same value, then it would sometimes be forced to remember that value, in order to follow this rule consistently. The resulting value would sometimes occupy a register, potentially preventing something more useful from being done with that register. As of LLVM 10, this “remembering” behavior can be achieved using the freeze instruction. A frozen undef (or poison) value is arbitrary, but consistent. So if we want to transform the shift function into the add function in a way that respects refinement, we can do it like this:

A general guideline is that an LLVM transformation can decrease the number of uses of a possibly-undef value, or leave the number of uses the same, but it cannot increase the number of uses unless the value is frozen first.
Instead of adding freeze instructions everywhere, one might ask whether it is possible to avoid undef-related problems by proving that a value cannot possibly be undef. This can be done, and as of recently Juneyoung Lee has added a static analysis for this. Alas, it is necessarily pretty conservative, it only reaches the desired conclusion under restricted circumstances.
Before concluding, it’s worth recalling that undefined behavior in an IR is not necessarily closely related to the source-level UB. In other words, we can compile a safe language to LLVM IR, and we can also compile C and C++ to IRs lacking undefined behavior. In light of this, we might ask whether undef, and its friend, poison, are worthwhile concepts in a compiler IR at all, given the headaches they cause for compiler developers. On one hand, we can find IR-like languages such as Java bytecode that lack analogous abstractions. On the other hand, as far as actual IRs for heavily optimizing compilers go, I believe all of the major ones have something more or less resembling poison and/or undef. The fact that a number of different compiler teams invented similar concepts suggests that there might be something fundamental going on here. An open question is to what extent these abstractions are worthwhile in an IR for a heavily-optimizing compiler middle-end that is only targeted by safe languages.
My colleagues and I believe that having both undef and poison in LLVM is overkill, and that undef can and should be removed at some point. This was not true in the past, but we believe that the new freeze instruction, in combination with poison values, provides adequate support for undef’s use cases.
4 responses to “Alive2 Part 3: Things You Can and Can’t Do with Undef in LLVM”
Are you saying undef should be removed in general, or only when the input language is a “safe” language?
Hi Matthew, we think it should be removed in general! When something like undef is needed, which is to say an arbitrary value but not a massively contagious thing, “freeze poison” will generally be good enough.
Ah, I see. Makes sense. Thanks!
How would the behavior of, and range of optimizations available from, undef differ from that of an abstraction model where a compiler could at is leisure process e.g. “x=y & z” by replacing downstream uses of “x” with “y & z”, if there was no evidence of any intervening action affecting x, y, or z, unless certain things were done with x that would “freeze” its value? The exact range of actions that would freeze a value could and likely should depend upon the intended usage of an implementation–optimizations that would be appropriate when an application will receive only trustworthy data may be inappropriate when building applications that will receive data from untrustworthy sources, but the kinds of optimizations that would be most useful would also be easiest and safest.
Suppose, for example, that the first field of a structure identifies which other fields have meaningful values, and a function wishes to create and store in a few places a structure whose third field has some value, whose first field indicates that only the first and third fields are relevant, and whose other fields are irrelevant. If the structure is an automatic object, and code sets the first and third fields of that object before writing it to other objects, it shouldn’t be too surprising if the compiler simply writes the first and third fields of those two other objects and leaves the other fields holding whatever they held previously. If, however, code that calls that function makes a copy of one of those structures, having the values of uninitialized fields differ in the original and copy, in part of the code far removed than the automatic structure object, would be rather more surprising.
Requiring that a compiler treat the act of making the first copy of the automatic structure object as freezing its value would impede what would likely be a useful optimization, but requiring that programmers wishing to uphold the Principle of Least Astonishment with regard to client code must explicitly initialize all structure members would likely necessitate making the machine code even less efficient. An abstraction model where returning from a function would by default freeze any objects written by the function, even if the function was in-lined, would likely offer a good balance between optimization and “astonishment”.