I believe that the central limit theorem provides a partial explanation for why it can be very difficult to create an effective random tester for a software system.
Random testing is carpet bombing for software: the more of the system you can hit, the better it works. The central limit theorem, however, tells us that the average of a number of random choices is going to follow a normal distribution. This is important because:
- Sophisticated random test-case generators take as input not one but many random numbers, effectively combining them in order to create a random test case.
- A normal distribution, whose probability decays exponentially as we move away from its center, is a very poor choice for carpet bombing.
An Example
Let’s say we’re testing a container data structure such as a bounded queue. It has a capacity bug that fires only when an element is added to a full queue. The obvious way to generate random test cases for a container is to randomly generate a sequence of API calls. Let’s assume that only the enqueue and dequeue operations are available, and that we generate each with 50% probability. How likely is it that our random tester will discover the capacity bug? The number of elements in the queue is just a 1-dimensional random walk, telling us that the probability will decrease exponentially as the capacity of the bounded queue increases.
What does this mean, concretely? If the queue is 64 elements in size and a random test case is 10,000 enqueue/dequeue operations, each test case has about a 90% chance of finding the queue bug by attempting to add an element to a full queue. This drops to 50% if the queue holds 128 elements, and to just a few percent if the queue holds 256 elements. Larger queues make it quite unlikely that this corner case will be tested.
In this trivial example, the central limit theorem is not so likely to bite us. We’ll probably notice (using a code coverage tool or similar) that the “enqueue on full” condition is not tested, and we’ll cover this behavior by hand.
Another Example
A while ago I posted this bit puzzle. I won’t repeat the problem description, but the quick summary is that the goal is to find an extremely efficient implementation for some fairly simple functions, each of which operates on a pair of bit vectors. The obvious way to test a function like this is to generate two random bit vectors and then inspect the output. In general “inspect the output” is tricky but it’s trivial here since my slow example code serves as an oracle.
But now let’s ask a simple question: given a pair of random 64-bit numbers, what is the Hamming distance between them? This is the distribution:
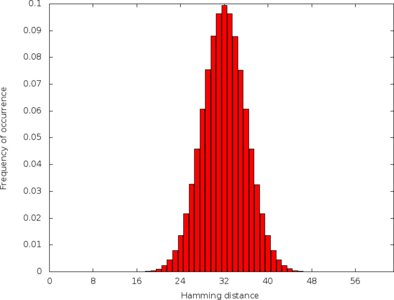
This is, of course, the normal distribution centered at 32. This distribution shows up here because each bit is effectively a separate random number, for purposes of the distance computation.
But why do we care? This matters because the functions of interest in my earlier blog post have a special case when the Hamming distance is 0. That is, when the input bit vectors are equal it’s not totally clear what to do unless you look at my reference implementation. In fact, if you read the comments you can see that a couple of people wrote buggy code due to missing this case. As the graph above makes clear, the probability of generating two 64-bit vectors whose Hamming distance is zero is quite low.
More Examples
Can we find more examples where the central limit theorem makes it hard to do good random testing? Definitely. Consider fuzzing a filesystem. If the API calls in a test case are equally likely to open and close a file, we’re not likely to reach the maximum number of open files. If a sequence of API calls is equally likely to create and remove a directory, we’re not likely to test the maximum number of subdirectories. Similar arguments can be made for almost any resource limit or edge case in a filesystem.
I suspect that normal distributions in test cases limit the effectiveness of Csmith. For example, since the number of local variables in a function is determined by many calls to the PRNG, we might expect this quantity to be normally distributed. However, certain numbers of local variables (I’m simplifying of course) cause interesting code in the register allocator, such as its spilling and rematerialization logic, to be called. Is Csmith adequately stress-testing that kind of logic for all compilers that we test? Probably not.
My hypothesis is that many similar effects occur at larger scale as we apply random testing to big, complex software systems. The larger the test case, the more likely it will be that some derived property of that test case follows a normal distribution.
Solutions
Here are some possible ways to prevent normally distributed properties from making random testing less effective.
First, we could try to execute an extremely large number of random test cases in order to saturate even parts of the space of test cases that are generated with low probability. But this is not the right solution: the rapid falling off of the normal distribution means we’ll need to increase the number of test cases exponentially.
Second, we can impose (small) arbitrary limits on system parameters. For example, if we test queues of size 4, we’re likely to reach the overflow condition. If we test bit vectors of size 8, we’re likely to test the case where the inputs are equal. This is an extremely powerful testing technique: by reducing the size of the state space, we are more likely to reach interesting edge cases. However, it has a couple of drawbacks. For one thing, it requires modifying the software under test. Second, it requires whitebox knowledge, which may be hard to come by.
Third, we can hack the random tester to reshape its distributions. For the queue example, we might generate enqueue operations 75% of the time and dequeue operations 25% of the time. For the bit functions, we can start with a single random 64-bit number and then create the second input by flipping a random number of its bits (this actually makes the graph of frequencies of occurrences of Hamming distances completely flat). This will fix the particular problems above, but it is not clear how to generalize the technique. Moreover, any bias that we insert into the test case generator to make it easier to find one problem probably makes it harder to find others. For example, as we increase the bias towards generating enqueue operations, we become less and less likely to discover the opposite bug of the one we were looking for: a bug in the “dequeue from empty” corner case.
Fourth, we can bias the probabilities that parameterize the random tester, randomly, each time we generate a test case. So, for the queue example, one test case might get 2% enqueue operations, the next might get 55%, etc. Each of these test cases will be vulnerable to the constraints of the central limit theorem, but across test cases the centers of the distributions will change. This is perhaps more satisfactory than the previous method but it ignores the fact that the probabilities governing a random tester are often very finely tuned, by hand, based on intuition and experience. In Csmith we tried randomly setting all parameters and it did not work well at all (the code is still there and can be triggered using the --random-random command line option) due to complex and poorly understood interactions between various parameters. Swarm testing represents a more successful attempt to do the same thing, though our efforts so far were limited to randomly toggling binary feature inclusion switches—this seems much less likely to “go wrong” than does what we tried in Csmith. My current hypothesis is that some combination of hand-tuning and randomization of parameters is the right answer, but it will take time to put this to the test and even more time to explain why it works.
(Just to be clear, in case anyone cares: Swarm testing was Alex’s idea. The “random-random” mode for Csmith was my idea. The connection with the central limit theorem was my idea.)
Summary
A well-tuned random tester (such as the one I blogged about yesterday) can be outrageously effective. However, creating these tools is difficult and is more art than science.
As far as I know, this connection between random testing and the central limit theorem has not yet been studied—if anyone knows differently, please say. I’d also appreciate hearing any stories about instances where this kind of issue bit you, and how you worked around it. This is a deep problem and I hope to write more about it in the future, either here or in a paper.
Update from evening of June 19
Thanks for all the feedback, folks! I agree with the general sentiment that CLT applies a lot more narrowly than I tried to make it sound. This is what you get from reading hastily written blog posts instead of peer reviewed papers, I guess!
Anyway, the tendency for important properties of random test cases to be clumped in center-heavy distributions is a real and painful effect, and the solutions that I outline are reasonable (if partial) ones. I’ll try to reformulate my arguments and present a more developed version later on.
Also, thanks to the person on HN who mentioned the law of the iterated logarithm. I slept through a lot of college and apparently missed the day they taught that one!
29 responses to “The Central Limit Theorem Makes Random Testing Hard”
Very interesting. Swarm is still pounding the center, but it’s a different center. In the trivial case, of course, when you get to one API call the “center” expands to fill the region.
Is there a way to get the good side of random but actually do well at generating things in the spaces like:
[mix of calls, with large number of opens]
1 close, well timed
Preferably, getting there without doing any concolic work, solving any constraints, etc. There is definitely an interesting class of bugs that want you to “swarm up to a point” then flip the switch on some turned-off feature. We may not have much idea how many such there are, because for things like compilers nobody really does that, and I doubt you find the bugs much without it, in some cases. For file systems, I know that classic random testing or swarm, or various explicit-state model checking strategies don’t really do this case well, and the constraint-solving doesn’t scale nicely.
I wonder if you could do some sort of GA with the –random-random idea.
It might also be interesting to extract the actual occurrences rates of artifacts in the generated bug cases. A step further would be to see how they change incrementally during the reduction process. Are some “regions” more likely to “loose” the bug (or turn into dead ends) than others?
Frankly, I’m not convinced that “why black-box testing has a hard time finding bugs” is really related to “the central limit theorem” (CLT); and your post contained nothing that could look like a proof, even very hand-wavy. The central limit theorem says that taking the average of a large number of variables distributed uniformly gives a normal distribution. In your case (random testing), what does “taking the average” corresponds to? This seems to be a fact about the iterated sum of distributions, and I do not see what the “sum”, as an algebraic operation, would correspond to in your setting.
Yes, when you try things at random, and plot some properties of those things that you decided in advance, you will often get normal distributions, because normal distributions are a very common case of “plausible” distributions. But is that necessarily a result of the CLT?
Without thinking much about the topic — you certainly have much more experience and hindsight — I would be that the central point about software system is that they have very localized discontinuities, that represent only a very tiny part of the search space; being heavily discontinuous in nature, they may be harder to spot than a defect of a physical system (if you fire an input *extremely close* to the buggy input, you still won’t see anything, while in a physical system you would observe a small deviation).
You do not mention white-box fuzzing at all. This is what I would think of to improve the efficiency of fuzzing, by taking the program semantics into account to detect those discontinuities and target them specifically (another way to see it is that you’re not looking at the *input* distribution anymore, but at the *computation* distribution, you’re trying to get a “program run” at random). Of course there are associated costs, because the white-box tools are less widely applicable, so I perfectly understand that you wouldn’t want to consider this kind of techniques.
Hi Gasche, you’re right that my post contains hand-wavy elements.
However, in some cases I believe the analogy is exact. Random walks are an extremely common behavior when executing a random test case, and the CLT (unless I’m misremembering) is the math that we would most naturally use to describe the probabilistic nature of a random walk.
If you don’t like CLT as a hard analogy, just take it to mean “the family of CLT-like results that cause normal distributions to appear everywhere in real life.”
I think automated whitebox testing is the best thing since sliced bread. However, I consider whitebox to be somewhat orthogonal to the kind of issue I talk about here. In reality, we’ll need to use both techniques. Furthermore, I’m kind of depressed that 4 years after the Klee paper, no open source whitebox fuzzer remotely scales to codes that I care about (compilers and similar).
Hi bcs, applying GA to tune the parameters would be really fun. However, the CPU requirements would be daunting and also we would have a strong risk of over-training. For it to work, we’d need to assume that all future compiler bugs will somehow look like the ones found in the training set. If the GA just helps us avoid doing really stupid things then this assumption may hold, but it’s not totally clear…
To amplify my previous comment, a GA will result in a positive feedback loop: it will bias the tester towards codes that have found bugs in the past.
But maybe we want to bias the other way. Maybe once we mine out the bugs in some region, we want to look elsewhere!
Alex and I have debated this a few times and come to no real conclusions. It’s tricky. In the meantime — lacking either intuition or data — I’ve been avoiding incorporating feedback into Csmith.
If you don’t like the CLT, well, just use Cauchy random variables instead 🙂 http://en.wikipedia.org/wiki/Cauchy_distribution But to bring the argument back on topic: there might be ways of controlling the randomization so you can prevent the concentration of measure.
If you can meaningfully talk about the desired probability distribution of test cases over the space of all possible programs, and all you have is a random walk, then perhaps you could use Gibbs sampling?
http://en.wikipedia.org/wiki/Gibbs_sampling
http://en.wikipedia.org/wiki/Metropolis–Hastings_algorithm
Hi Carlos, the Cauchy distribution kind of reminds me of the delta function, which I have to admit screwed with me all the way though a PDE class.
Regarding uniform (or whatever) sampling of the space of test cases, this is easy in certain cases but extremely hard generally. Suresh and I talked about it a few years ago and failed to come up with a good answer. Techniques like Swarm testing are basically efficient ways to get some of the benefits of uniform sampling.
I’ll read up on Gibbs, thanks for the links!
Re: GA, this is great analogy to biology in that tuning a population for one environment, while ideal for the individual is detrimental to the population because it inherently makes them unfit in the face of change. (Ironically, I expect this is another manifestation of the Central Limit Theorem.) But that answer is the same, diversity and differentiation of species.
As for compute power, that’s cheap, bordering on free, if you get the right people interested in helping.
I think your idea has some merit, but you can’t defend it with fluff like “However, in some cases I believe the analogy is exact.” Excise phrases like that from your vocabulary.
> As for compute power, that’s cheap, bordering on free, if you get the right people interested in helping.
I think exponentially more compute power isn’t free, even though random testing/swarm is about as good for parallel execution as one can imagine.
@Daniel Lyons: I would agree with you in some cases, namely things more scholarly than a blog or comment.
Hi Alex, bcs works at a location that doesn’t have infinite compute power, but does have the next best thing.
@Alex Groce: Overcoming the Central Limit Theorem via brute force requiters exponential compute. Running a GA pass on the randomness factors of a fuzzer would (one hopes) require somewhat less.
Fair enough. 🙂
Still, some outliers are so outlierish in some distributions that it’s hard to imagine hitting them even if we turned every electron in the known universe into a little random testing engine. We probably need better distributions even with lots more computer power.
bcs: Agreed, I think GAs/learning in general has some applications here, though the difficult bit is that ML/GA has trouble with “exploration” to hit targets unlike anything thus far generated, where the set of targets isn’t known in advance.
bcs, alex: What about using ML to optimize for coverage, as opposed to optimizing for bug-finding? This gives a much finer-grained fitness function…
Coverage as in of the tuning-factor-states-space or code coverage of the system under test?
That’s what people have done, like Jamie Andrews’ Nighthawk work (or my own ABP-based stuff). It’s useful, though we probably need more solid evidence that chasing certain coverage targets is a good goal. But if it works, at least chasing complete branch coverage seems like a worthy goal, and non-trivial.
I was thinking branch coverage of the SUT. This is a pretty good kind of coverage but still cheap to measure.
Random thought: where in the tuning-factor-states-space are bugs most likely to be found? What measurable properties could be looked at? In particular, I’m thinking should the fuzzer seek out localities that tend to give highly variable SUT coverage?
to be a bit pedantic, it is the binomial distribution around 32.
yonemoto, thanks! I appreciate pedantic comments that contain information.
A fifth option that I employ is to use operational data to bias the fuzzer. This seems to be effective to find the “garden variety” bug.
Hi Tim, definitely. In the case of Csmith we have literally spent years tweaking and tuning things to make it more effective.
First of all, you need to explain the probability space and more importantly the random variables in the probability space where the CLT is invoked. I suppose you are using the Lindeberg’s condition, therefore do ensure that the random variables satisfy the condition.
Honestly, what you are doing here is a little bit fishy.
One obvious improvement would be to use some knowledge about the program under test. For this see e.g. ftp://ftp.research.microsoft.com/pub/tr/TR-2007-58.pdf
Without such extra knowledge you might still hope that the situation that provokes the bug is in some sense simple, because the program under test is small (in comparison with the space of all possible inputs) or because you can only understand simple bug reports. If the situation is simple it should have a small description in the sense of Kolmogorov complexity, so it should be feasible to generate it at random by generating random descriptions in some rich enough language that describes programs that generate test inputs. Presumably there is a tradeoff between having a rich enough language to make bugs accessible and having a language that describes programs that run forever without generating any inputs. This is also a rational for GA approaches.
Another reason for one sort of random testing comes from SWEBOK: In helping to identify faults, testing is a means to improve reliability. By contrast, by randomly generating test cases according to the operational profile, statistical measures of reliability can be derived. Using reliability growth models, both objectives can be pursued together (see also sub-topic 4.1.4 Life test, reliability evaluation).
The general observation here being that hits, not attempts, are what follows the central limit theorem; therefore the presumption that the edges are lower value because they are less frequent than the center is in error, because it is for that very reason that finding them becomes so difficult, and using a tool which can find them automatically with some regularity just by running it for a long time becomes so useful.
If you imagine the problem space to be an eight real-valued dimensional space, and thus unsearchable, it is revealed that the problem is merely a programmer with unrealistic code expectations.
Oh no, something that *only* finds very difficult errors on its own occasionally? How /terrible/!
I think the real problem is the infinite sampling space.
In the hardware world, you can get quite close to bug free using random testing + fascist coverage goals (not just line coverage – last time I was involved, there were about 10 different coverage metrics which each had to be satisfied – or signed off in blood – for every bit of the code). Anything which smacks of infinite test space ( eg, involves a datastructure) is punted into software, not because you couldn’t implement it, but because it would have too high a chance of having bugs you didn’t find before tapeout.