Many computer scientists, including myself, end up doing research that needs to be evaluated experimentally, and yet most of us have had little training in statistics or the design of experiments. We end up teaching ourselves this material as we go, which often works pretty well. On the other hand, sometimes the issues are surprisingly subtle. Today’s piece is about a example where I’ve found this to be the case; I ran across it a few years ago when some sanity checks on confidence interval code weren’t giving answers that seemed to make sense.
The topic is confidence intervals for a binomial proportion, where we take a series of independent yes/no measurements and use them to compute an interval that most likely contains the true proportion. For example, if we flip a coin 50 times and get heads 28 times, should we conclude that the coin is biased towards heads? In other words, does the confidence interval for the proportion of heads exclude 0.5? In this case, the 95% interval does contain 0.5 and so the data does not support the conclusion that the coin is unfair at the 95% level.
If we reach some conclusion with 95% confidence, what does that actually mean? Informally, it means that if we repeated the entire experiment (in this case, 50 coin flips) many times, we would reach the correct conclusion 95% of the time. The other 5% of the time we would be incorrect. Statisticians formalize this as the coverage probability: “the proportion of the time that the interval contains the true value of interest.” At this point most of us would ask: Doesn’t the 95% confidence interval have a coverage probability of 95% by definition? Turns out the answer is “no” and this is where the fun starts.
Let’s take an example where n (the sample size) is 21 and p (the true proportion) is 0.479. We can empirically compute the coverage of the 95% confidence interval by repeatedly taking 21 random samples and seeing if the true proportion lies within the 95% confidence interval. For now we’ll use the normal approximation to the binomial. Here’s some code that does all this. Compile and run it like so:
$ gcc -O conf.c -o conf -lm $ ./conf 21 0.479 n= 21, p= 0.479000, nominal coverage= 95.00 % measured coverage= 91.62 % measured coverage= 91.63 % measured coverage= 91.63 % measured coverage= 91.61 % measured coverage= 91.60 %
As we can see, the coverage is about 91.6%, which means that although we asked for a 5% probability of error, we are actually getting an 8.4% chance of error—a pretty significant difference. There are a couple of things going on. One problem is that the normal approximation is not a very good one. In particular, it is not recommended when np or n(1-p) is less than 10. Here, however, we pass this test. Other sources give a less conservative test where np and n(1-p) are only required to be 5 or more, which can lead to coverage as small as about 87.4% (for n=11, p= 0.455).
The unfortunate thing is that many stats classes, including the one I took many years ago, and also books such as the ubiquitous Art of Computer Systems Performance Analysis, do not go beyond presenting the normal approximation—I guess because it’s so simple. However, if you use this approximation and follow the np>5 rule, and aim for a 95% confidence interval, you could easily end up publishing results that are not even significant at the 90% level.
Many statisticians recommend avoiding the normal approximation altogether. But what should be used instead? The Clopper-Pearson interval is fully conservative: it is guaranteed to never have less coverage than you asked for. However, it is often overly conservative, so you might be getting 99% confidence when you only wanted 95%. What’s wrong with that? First, it may lead you to waste time running unnecessary experiments. Second, it may cause you to reject a hypothesis that actually holds at the desired level of confidence.
In my work for the last several years I’ve used the Wilson score interval. It is hardly any more difficult to implement than the normal approximation and has better behavior for small np. Also, it works for p=0 or p=1. The Agresti-Coull interval also has many good characteristics. Agresti and Coull’s paper from 1998 is short and easy to read for non-statisticians, I’d recommend it for people interested in learning more about these issues. A more exhaustive (and exhausting) discussion can be found in a 2008 paper by Pires and Amado.
Earlier I alluded to the fact that the normal approximation was just one problem with creating a confidence interval for a binomial proportion. The other problem—and it is a problem for all approximations, including the “exact” Clopper-Pearson interval—is that since the binomial distribution is discrete, it is not possible in general to make the actual coverage probability be the same as the nominal coverage probability.
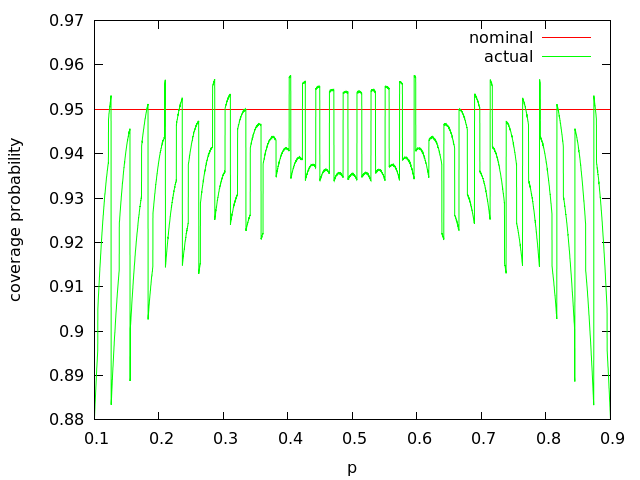
The relationship between the nominal and actual coverage probabilities is interesting to observe. The following graph (produced using the C program above) shows the behavior of the normal approximation of the 95% confidence interval for n=50, between the np=5 and n(1-p)=5 bounds:
I wrote this piece because the difference between nominal and actual coverage probabilities, which is well-understood by statisticians, does not seem to have been communicated effectively to practicing scientists. In some ideal world the details wouldn’t matter very much because people like me would simply rely on a convenient R library to do all confidence interval computations, and this library would be designed and vetted by experts. In practice, a one-size-fits-all solution is probably not optimal and anyway I always seem to end up with confidence interval code embedded in various scripts—so I’ve spent a fair amount of time trying to learn the underlying issues, in order to avoid screwing up.
Summary: Ignore what you probably learned about confidence intervals for proportions in college. Use the Agresti-Coull interval or Wilson score interval.
6 responses to “Gaining Confidence in Confidence Intervals”
Nice! This sort of content is exactly what I was hoping for from the Evaluate effort (http://evaluate.inf.usi.ch/ ), though it’s still in its early days.
Another related statistical topic for experimental people (at least that I’ve run into) is the inappropriate use of certain statistical models (e.g., just comparing means) for data that is not uniformly distributed. My experimental data (benchmark runs), tends to be either bi- or tri-modal and I’ve had to resort to different tests to gain confidence in whether or not my optimizations actually helped, harmed, or left the benchmarks alone.
I’m not sure any reviewers really cared, unfortunately.
In the Social sciences there is something like a 70% probability that some dataset will have a normal distribution, also a lot of error analysis assumes a normal distribution irrespective of the underlying distribution (because the analysis is simpler).; in the past most stats books have been aimed at the social sciences and distribution tables/methods are readily available for the normal distribution. These coincidences have combined to lead to a ‘use normal’ for everything approach.
These days we don’t have to rely on precomputed tables, we can let computers do the work.
I’m working on a book on empirical software engineering and one of the questions I’m trying to answer is “What is the most common distribution in software engineering?” The normal distribution is very rare in the datasets I have, exponential is common and negative binomial is popular in places. I have not looked into whether measurement errors are normally distributed.
Incidentally, why is that plot so spiky? In fact even the spike end -point don’t look right. From your description I was expecting more lines to be present.
Hi Lars, I hadn’t seen the Evaluate project, thanks for pointing it out. Raising the bar for statistical analysis in software systems is a good thing. As you point out, at the moment one cannot count on the reviewers to appreciate a good job.
On the other hand, I think some skepticism of statistical methods is useful. Using your example of compiler optimization, a real danger is that I do an awesome job at the stats but miss out on the fact that my effect is totally due to some quirk of the Linux scheduler or the cache setup on some random CPU.
In other words, awesome stats are mostly needed when effects are small and people rightfully mistrust results in computer systems where the effects are small since these are most likely not portable to other systems.
Hi Derek, I haven’t attempted to understand the reasons for the funny shapes in the plot. However, I am fairly confident that it is correct and you can check over the code yourself if you want. The character of the plot is very similar to what we see in other papers on this topic such as the two that the article links to.
In addition to using good confidence intervals, I would suggest to prefer order statistics when possible, because they are more robust. That is, use the median rather than the mean. One advantage is that there are exact confidence intervals for order statistics, which do not depend on the underlying distribution.
Assume you have measured p in 10 independent experiments, and received (in some order) the values p₠≤ pâ‚‚ ≤ … ≤ pâ‚â‚€. Then you could publish (pâ‚… + p₆)/2 as the median probability. Also, you know that with 97.9% probability, the true median probability lies between pâ‚‚ and p₉. This is true independent of the underlying distribution; you don’t need to know that p is the probability of a binomial distribution, and you don’t need Gaussian approximations.
Other people explain this much better than I do; please refer to Jean-Yves Le Boudec’s book on performance evaluation [1] or on the R mailing list [2].
[1]: http://perfeval.epfl.ch/
[2]: https://stat.ethz.ch/pipermail/r-help/2007-February/124958.html
In hindsight, I realize that I proposed a solution for a slightly different problem, and that quantiles are probably not applicable to experiments with a binary outcome, such as the one that you are describing. They remain a valuable tool for other types of experiments, though.